This is an archived page and is no longer updated.
Please visit our current pages at https://rvs-bi.de

Hazards, Risk and Incoherence

Peter B. Ladkin

Article RVS-Occ-98-01
I consider some standard engineering definitions of hazard, accident and risk, and show on a simple example how the definitions of hazard and risk are deficient.

Contents

Introduction

 Back to Contents

Today's complex systems, from desktop computers to fly-by-wire airplanes, may fail in all sorts of ways, some of them merely annoying and some of them downright dangerous. The study of system safety is concerning with identifying and mitigating the dangers of using a system, whether these dangers are inherent or caused by failure.

It is necessary in a scientific study of a phenomenon to try to be as precise as possible in describing it. Leveson notes that terminology in system safety has not always been used consistently (Lev95, p171), and gives a series of definitions of such terms as reliability, failure, error, accident, incident, hazard, risk and safety (Lev95, Chapter 9: Terminology), which attempts to do the most justice to the engineering definitions, and is the result of considerable research into the engineering literature over seven years or so (Lev98p). We may, with gratitude to Leveson for her scholarship, take these as definitive (Footnote 1).

Having said that, I shall show by means of a simple example how the definitions of hazard and risk fail.

There are alternative concepts of hazard to that endorsed by Leveson. I shall also note that these do not perform the required function.

Systems, Objects and Behavior

Back to Contents

A standard way of looking at the world, enshrined nowadays in formal languages and methods for reasoning, is that there are objects which have properties and relations to other objects, which properties and relations change with time. (One says, if the properties change, that the object has changed. If only its relations change, this is usually not taken to entail that the object has changed.) The way that the properties and relations of an object or collection of objects change with time (including their relations to objects not in the group) can be called their behavior. This ontology of objects, properties, relations and behavior is enshrined in most formal semantics for understanding systems; for example, the language of temporal logic.

A system may be defined as a collection of objects with behavior. We can make a further distinction between systems which occur naturally, and artifactual systems, built by humans or animals to serve a particular purpose (Sea95); teleological systems, if you will. Engineering is broadly concerned with teleological systems, as in the definition of Leveson (Lev95, p136):

A system is a set of components that act together as a whole to achieve some common goal, objective, or end. [....] This concept [....] relies on the assumptions that the system goals can be defined and that systems are [....] capable of being separated into component entities such that their interactive behavior mechanisms can be described.

Although the entire universe can be considered as a single system (the collection of objects = everything; relations and properties = all relations and properties), this is not the system mostly considered by engineers; there are considerable doubts even whether it is a teleological system. Mostly, one considers smaller parts of the universe; hence one may make a distinction between those objects that belong to the system and those that do not. This distinction leads to the notion of the system boundary, namely the distinction between what objects and behavior are to be considered part of the system and which not. The number and types of objects are not fixed; some of us believe there are more objects than others do. For example, `platonist' mathematicians judge mathematical entities such as the numbers 1,2,3,.... to be real objects, and `nominalist' mathematicians argue that these are not real `things' but are syntactic constructions involved in ways of speaking about operations one performs on physical objects. Another common view is that parts of objects are also objects; the question here is what parts there are. There is a logical science, mereology, concerning which parts of objects exist. One widely-accepted mereological operation is that of fusion, whereby from objects X and Y is formed the object X+Y, the `mereological sum', which has X and Y as parts, and such that any object with X and Y as parts has also X+Y as a part: the `smallest' object one can make from X and Y in other words. Suffice it to say that there is enough ontological and mereological science around to populate the universe with as many, or as few, objects as one thinks should be there, and enough system parts to satisfy the most baroque, or few enough to satisfy a minimalist, taste.

What about the objects in the universe that are not part of the system? Some of them constitute the system environment, which is normally taken only to be that part of the universe which, while not being part of the system, may nevertheless influence or be influenced by the behavior of the system. There are some who think that no reasonable distinction may be drawn between those parts not of the system that are susceptible to influence and those not-parts that are not susceptible; they can feel free to take the environment of a system to be the entire rest of the universe; the point of this paper does not depend on it.

How may one describe behavior? Behavior is distinguished by enumerating the change in properties and relations of objects, and one can attempt to describe it by attempting to describe change. Let a state of a collection of objects be the collection of all properties and relations which hold of those objects at a particular time. This is a crude definition, but it may be made more precise using the kinds of formal languages common since Frege. Since behavior is a change in these properties, it results in a change of state; some properties or relations of the objects held previously, and after the change do not (or others hold). One may therefore describe a change by describing the `before' and `after' states, or parts of them, or relations between them. Changes may also be `strung together', to form more complex descriptions of behavior over time, sometimes called processes.

The Definitions

Back to Contents

Given these basic concepts of system, change and behavior, one may talk about how a system attains or fails to attain its goals. Leveson defines (Lev95, p172):

Reliability is the probability that a piece of equipment or component [of a system] will perform its intended function satisfactorily for a prescribed time and under stipulated environmental conditions. [....] Failure is the nonperformance or inability of the system or component to perform its intended function for a specified time under specified environmental conditions.
It should be clear that both definitions concern teleological systems. However, the notion of safety is not so restricted: (Lev95, pp172,181):
An accident is an undesired and unplanned (but not necessarily unexpected) event that results in (at least) a specified level of loss. [....] Safety is freedom from accidents or losses.
In order to use these definitions, one has to specify what one considers to be losses (and their levels). Such losses are often specified as numbers of deaths or injuries, financial losses to concerned parties, damage to the natural environment, and so forth. Typically, there is considerable agreement on what is to be considered a `loss' (for example, deaths, injuries, money, damage), and how the levels are measured (mostly by numbers; more generally on ordinal or ratio scales (KLST71)). Leveson notes that this is stipulatory: as far as systems science is concerned, it is up to us to specify what we consider a loss and what levels constitute an accident.

There is nothing in the definition of accident concerning the system boundary; we may presume that many accidents involving both system and environment occur, and are thus described. This is intuitively reasonable; the airplane crumples and dismembers, not randomly but because the mountain rose through the mist to smite it. With teleological systems, we may be presumed to have more control over the constitution and behavior of the system -- it is after all our artifact -- than we may over the environment. The aircraft can be engineered to predict the looming presence of the mountain and fly above it; it is considerably harder to move the mountain out of the way of the encounter. Accordingly, we shall wish to speak about the part of the system that contributes to an accident, even though given favorable environmental conditions the accident will not occur: if the aircraft flies at or above a (true) 30,000ft (above mean sea level, MSL) altitude, there will be no mountain for it to encounter; if it flies through the Himalayas below 28,000ft MSL, there are some places it cannot fly without meeting an obstacle. Accordingly, we can distinguish a state including an altitude of less than 28,000ft MSL over the Himalayas as potentially leading to an controlled-flight-into-terrain (CFIT) accident, in the absence of knowledge of exactly where the aircraft would fly.

Such considerations motivate the following definitions (Lev95, pp177-9):

A hazard is a state or set of conditions of a system (or an object) that, together with other conditions in the environment of the system (or object), will lead inevitably to an accident (loss event). [....] A hazard is defined with respect to the environment of the system or component. [....] What constitutes a hazard depends upon where the boundaries of the system are drawn. [....] A hazard has two important characteristics: (1) severity (sometimes called damage) and (2) likelihood of occurrence. Hazard severity is defined as the worst possible accident that could result from the hazard given the environment in its most unfavorable state. [....] The combination of severity and likelihood of occurrence is often called the hazard level. [....] Risk is the hazard level combined with (1) the likelihood of the hazard leading to an accident (sometimes called danger) and (2) hazard exposure or duration (sometimes called latency).
So a hazard, flying under 28,000ft MSL, in combination with other conditions in the environment (doing so in a particular direction in a particular geographical location, so that impact cannot be avoided) will inevitably lead to an accident (loss of airplane and death or injury of occupants) that may be more or less severe, depending on how many people on board there are, how expensive the aircraft is, what environmental damage is sustained, and so on.

It is important to note that this concept of hazard divides states of the system into two classes, consisting respectively of those states in which the aircraft is flying at an altitude greater than that of the obstructions in the vicinity; and of those in which the aircraft is flying at or below that altitude. The first category of states will not (because they cannot) lead to a CFIT accident, and states in the second category allow the potential for that kind of accident. Accordingly, the states in the second category are hazard states for CFIT, and those in the first category are not.

To take another example: an aircraft flying through cloud with the potential for embedded thunderstorms actually encounters one. The hazard consists in flying through cloud with embedded thunderstorms (rather than flying clear of such weather); the severity is loss of the aircraft and occupants; the `most unfavorable state' of the environment is a thunderstorm of sufficient power to upset the aircraft and cause breakup under aerodynamic loads; the danger is how likely one is to fly through such a thunderstorm while flying through the stormclouds; and the duration is the length of time one flies through the stormclouds. One could presumably measure the relevant probabilities (likelihood and danger) by measuring the spatial distribution of thunderstorms in stormclouds of the given type, and the frequency of severe ones. All well and good. But do these concepts work generally?

The System

Back to Contents

Consider the following universe. There are three objects x, y and z -- let us call them `atomic objects' -- and thus x+y, x+z and y+z also, if you're a mereological profligate. There are precisely three properties that may apply to any atomic object, which I shall write using standard formal notation, and I shall call 1, 2, and 3. Furthermore, these properties hold exclusively of each object: if 1 holds of x, then 2 and 3 don't hold, and mutatis mutandis for 2, 3 and y and z. Hence the state of the universe may be described by specifying which property holds of which object. The collection of possible `atomic' assertions is thus

1(x), 2(x), 3(x), 1(y), 2(y), 3(y), 1(z), 2(z), 3(z)

and, of these, precisely one involving a given object is true in any state. I can represent the state

1(x) and 2(y) and 1(z)

by the abbreviation

121

similarly, the state 3(x) and 1(y) and 2(z) by 312 and so on. The collection of all possible states is thus

111, 112, 113, 121, 122, 123, 131, 132, 133, 211, 212, 213, 221, 222, 223, 231, 232, 233, 311, 312, 313, 321, 322, 323, 331, 332, 333

I call S along with its environment the `universum'. The possible changes of the universum are similarly simple: a change is possible from property 1 of any object to property 2 of that object; and from 2 to 3; no other changes are possible. Let us also assume that changes are discrete: that no two changes happen simultaneously (this assumption is for convenience only, as noted in Section Trying To Fix It below; giving it up just complicates the arithmetic). I assume that any possible change in state has an equal probability of happening. Thus in the state 112, changes resulting in states 212, 122 and 113 have each a probability 1/3 of happening; while in state 213, changes resulting in states 313 and 223 each have probability of 1/2, because no change is possible to z. I also assume that probabilities of transition are dependent only on what current state the universum is in: history is irrelevant.

Finally, I define a system S consisting of objects x and y; z constitutes the environment/rest of the universum. (This also means, if one so wishes, that S contains the object x+y; and that there are mixed objects, part system, part environment, namely x+z and y+z. These ontological niceties need not concern us, since any properties of these objects may be defined logically from the properties of x, y and z.) The system is teleological: it starts in state (11-), namely system state (1(x) and 1(y)), its goal state is (13-), namely universum states 131, 132 or 133, and state 123 is a loss with a severity of unity (since it is the only loss). I assume there is an equal probability of S starting in any state of the environment; 111, 112 and 113 are equiprobable universum states for the start of S, each with probability 1/3.

S works as follows. It starts in state (11-) and `runs' (changes state) until no more actions are possible. As it changes, so does the environment. I suffer loss if the universum passes through state 123, and I consider S to have succeeded if it passes through state 13- without me having suffered loss. We shall see that S is not very reliable (the probability of attaining its goal is about 1/10), and the chances of loss are quite high (about 1/3).

This system, indeed this universum, is just about as simple as could be. It is finite, with finitely many states and finite (terminating) behavior. We may see how the definitions given so far apply to this system. If we expect them to work in describing complex systems, we should be able to use them to describe such a simple system as S.

The Problems

Back to Contents

The behavior of the universum may be seen in the figure below. This figure is also provided in Postscript so that it may be viewed concurrently with the text with an appropriately configured browser.

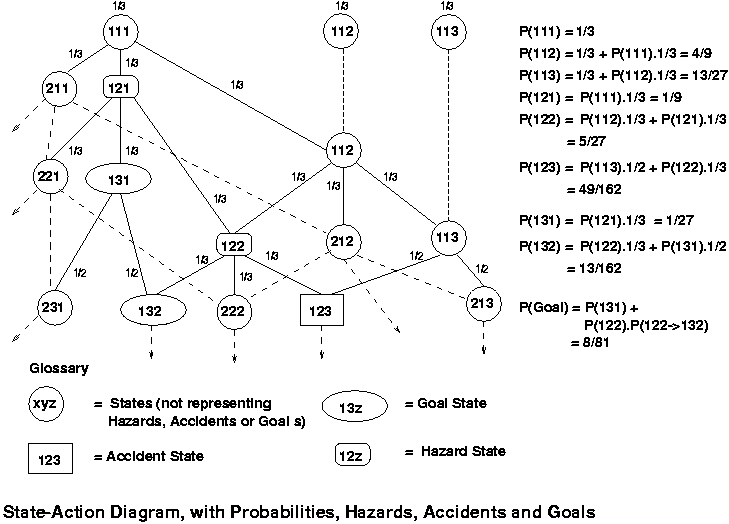
Figure: State-Action Diagram of System S

States of the universum are shown in circles, with system goal states shown as ovals; the loss state as a larger rectangle; and the hazard states as boxes with rounded corners. One should observe that one can attain the goal state 133 only by passing through 132, already a goal state, or through 123, the `specified level of loss' state. We may regard 131 and 132 as the two goal states that count, since in order to reach 133, we would have either achieved our goal already or suffered an accident. Since I am not primarily concerned with reliability, this observation has no bearing on my main points. The three initial states are 111, 112 and 113; each has probability 1/3. From state 111, the universum may progress to 112, 121, or 211 with equal probability. Since the loss state is 123, of which the system part is (12-), a state satisfying 1(x) and 2(y) is a hazard state; namely states 121, 122. This conclusion will be further justified in the next section.

Is state 123 itself a hazard state? Not according to the definitions; for 123 is the loss state and an accident is defined as an event that results in a loss. Accordingly, there are two sorts of accident events, namely the transitions 122 -> 123 and 113 -> 123. Since a hazard state is a state which, coupled with the worst possible environmental state, leads to an accident, a hazard state must precede an accident event; accordingly it precedes 122 -> 123 and 113 -> 123, thus must be or precede 122 or 113, since there are no loops. State 123 cannot occur before an accident event which results in it. It follows that the states of the universum in which the system is in a hazard state are 121 and 122 only.

Note that the system can have an accident without going through a hazard state: the change 113 to 123 is an accident, but the system state (11-) is not a hazard state. This is because the worst possible state of the environment is 3(z), which together with (11-) yields universum state 113, and an accident is not inevitable from this state: the universum could transition to 213 instead with equal probability (1/2). Inevitability of an accident in the worst environment state, however, is part of the definition of hazard state. It follows that (11-) is not a hazard state. This conclusion will be considered further below.

Clarifying `Hazard'

Back to Contents

The system S is a teleological system: goals are stipulated. One characteristic method of stipulating the boundary between teleological system and environment is to consider which features of the universum one can more or less control, and which not, and to make the decision on this basis. I shall call the assumption, that the decision to place the boundary is made more or less consistently with this criterion, the boundary assumption.

For example, the state of a runway surface may be controlled to some degree: one can clear it of debris, or excess water or snow, and direct traffic elsewhere until such time as it has been accomplished. In contrast, one has little or no control over the weather at the airport and hence the dynamic conditions of the air through which landing and departing aircraft fly. Under this criterion, it would be appropriate to consider the runway condition part of the system, and the weather not, and the (expected) behavior of the system varies accordingly. Although one is obliged simply to wait until bad weather changes for safer flying conditions, it would be an inept (or impoverished) airport manager who simply waited for the snow to melt from hisher runway.

The definition of hazard refers to a system state that, together with other conditions in the environment, will lead inevitably to an accident. An accident is not necessarily inevitable from a hazard state, but if the environment doesn't cooperate, it is. What exactly does the phrase `conditions' mean? One way to interpret it would be as a state. In my example S, I interpret it as state or behavior, hence prima facie I need to justify this choice, which I shall now do.

There are two related reasons for this choice. One is that a `condition' is to be interpreted as any state predicate whose value remains invariant for a period. Another is that, under the boundary assumption, one cannot expect the environment to remain static, and cannot control its mendacious behavior. One can, however, remark mendacious behavior patterns, and define a state predicate to indicate that the environment is indulging in these patterns. I argue that the notion of `condition' should include this stance towards such behavior patterns.

Consider the previous example of an aircraft flying through cloud with the potential for embedded thunderstorms. A thunderstorm, and its associated electrical discharges, solid and liquid precipitation, and violent air movements, is a rapidly changing weather phenomenon. Storms are classified for the flying community in terms of various numerical levels, with Level 5 being a very severe storm. A storm at Level 3 should be closely observed, and any Level 4 or 5 storms should be avoided. Descriptions of the levels are available, in terms of their potential for and likelihood of behavior that would be deleterious to aircraft encountering the storm. Logically, a classification system is a definition of new state predicates. These state predicates remain invariant throughout certain behavior: for example, now it is hailing golfballs, thirty seconds later it isn't; now there is a severe microburst, one minute later it is over; but these are all common behavior for a Level 5 storm and to be more or less expected. Accordingly, throughout this rapidly changing behavior, the storm is persistently classified as Level 5, and this persistent state information leads to certain behavior from the air traffic system (more particularly, its human operators), that is different from the behavior of the system were the storm to be Level 3. I take it as appropriate to consider such classifications `conditions' for the purpose of the definition of hazard.

I might further suggest that such schemes are the stereotype of what is meant by `conditions'. I have presumed that the environment of a system is a a part of the world over which one has little control. One must nevertheless find ways of describing it. We have ways of describing persistent features, as well as changes in those features: thus predicates, and changes in value of predicates. A state may also be stipulated: any particular collection of values of the predicates in which we are interested. States and their changes are under this view a general means of describing the world, and specifying states by defining new state predicates is a creative act. In logical terms, the state predicate defining the condition is invariant throughout certain behavior. This invariance enables the condition to persist for a suitable period of time, and allows us to use it to determine how a system should behave in its presence, and to attempt to incorporate that into the system design. The creation of state predicates is a form of abstraction: a way of paying attention to certain features of the situation while ignoring others.

This does not mean, of course, that the environment does not exhibit change with respect to these new state predicates. Of course it does. In a famous accident at Dallas-Fort Worth airport in the 1980's, in the time that it took a weather observer to visit the bathroom, a Level 2 storm on the approach path changed into a Level 4 storm; one of the most rapid changes in status ever observed. Accordingly, it turned rapidly from an apparently benign weather phenomenon into a danger, causing the upset and destruction of a Delta Airlines L-1011 that flew threw it.

I conclude that `condition' in the definition of hazard refers to a state predicate that may remain persistent under observed environmental behavior. The environment may thus remain in a specified `condition' while exhibiting behavior; the condition is invariant with respect to this behavior.

For system S, the two conditions of the environment I shall consider are

Intuitively, the second condition is a process that subsumes the first, in the sense that the first condition occurs as a subprocess of the second. An example would be an extreme microburst that occurs as a subprocess of a Level 5 thunderstorm: the condition of there being a microburst and that of being a Level 5 thunderstorm are related similarly to conditions C.1 and C.2 of the System S environment.

We can precisely define the notion of subsumption for conditions as follows. First, some preliminary definitions. Suppose C and D are processes; that is, sequences of alternating states (defined by the values of state predicates) and transitions between states. I have already noted that the transitions between the states can be defined by specifying `before' and `after' state predicates, or a relation between them. Accordingly, only the specification of the sequence of state predicates is necessary to define a process, and I consider a process here to be defined by the sequence of states. I define:

It requires a word of explanation as to how a state can imply another one, and how the definition of specialisation uses that feature. I have already explained the notion of state as being distinguished by a state predicate. For the system S, I described the predicates that could be true, and distinguished the state of the universum by the collection of combined values of the predicates. I have pointed out above that one can also create new state predicates by definition. Accordingly, states are distinguished by the values of the predicates that are true. Thus to each state C corresponds the conjunction of all true state predicates ConjPred(C) (this may be an infinite conjunction if the number of distinct state predicates is infinite. I take it this causes no problems). C implies D means simply ConjPred(C) logically implies ConjPred(D). I take it that the notion of logical implication needs no explanation here. Specialisation means that each state in D occurs as a part of a corresponding state in C. That entails that the state predicate describing a given state in C must include a conjunct describing the part that is D. It follows that the states in C imply their counterparts in D, according to the notion above.

Now I may define the notion of subsumption. Condition C subsumes condition D just in case

For completeness, I enumerate all the other conditions of System S:

I leave it as an exercise for the reader to determine the subsumption relations between these conditions and between these and conditions C.1 and C.2.

Finally, I should clarify the notion of `leading to an accident' in the definition of `hazard'. The symbol `/\' shall denote conjunction. I define: a condition `leads to' an event or process if it subsumes it. Thus, a system state P together with a condition C of the environment `inevitably leads to an accident' if there is an event Q -> T subsumed in C such that (P /\ Q) -> (P /\ T) is an accident.

It can be seen from these clarifications that (12-) is a hazard state of the system: the conjunction with C.1 or C.2 leads inevitably to an accident. In contrast, (11-) is not a hazard state: there is no condition of the environment, the conjunction with which inevitably leads to an accident, as can be seen by trying all the conditions enumerated above. In order for an accident to occur, the system itself must make a transition; namely to the state (12-).

The system S is so defined that it cannot attain its goal without performing such an action leading it into a hazard state or a loss state, but this is logically incidental. System S is not a system in which any degree of control is apparent, but one engineering purpose of distinguishing hazard states is in general to allow some degree of system control to come into play, where it exists. Under the boundary assumption, one may expect to exercise more control over system states and over system transitions than over those of its environment. Accordingly, one distinguishes system states that, in conjunction with conditions in the environment, lead to accidents, from those which do not. Aircraft that do not take off do not have CFIT accidents; however, simply taking off is not normally regarded as a hazard state for CFIT because there are usually many other system states that must intervene in order for a CFIT accident to become inevitable. Taking off does not, in conjunction with environmental conditions, lead inexorably or even probably to a CFIT accident. The exception would be when the takeoff performance of the aircraft does not suffice to avoid terrain and other obstacles; the accident becomes inevitable by trying to take off. In this case, being in takeoff mode is indeed a hazard state; and it is part of the system, namely the regulations (for example, the U.S. Federal Aviation Regulations), which explicitly require the human part of the system, the pilot, to determine that takeoff performance is adequate. In our terminology, the pilot is required by regulation to ascertain that taking off is not a hazard state. Thus is system control exercised, and this exception clarifies the rule for use of the concept of hazard espoused by Leveson.

From Hazard to Loss

Back to Contents

The universum states corresponding to the system initial state (11-) have equal probability of occurring as the initial state in the system's behavior. Since transitions occur discretely, the probability of occurrence of a specific system behavior may be obtained by multiplying together the probabilities along the path of transitions that the system takes.

What is the likelihood of occurrence of the hazard state? That would be the likelihood of occurrence of 121 together with the likelihood of occurrence of 122. There is only one transition, from 111, that leads to 121. The probability that the system takes this path is the probability that it starts in state 111, P(111), multiplied by the probability of its taking the transition from 111 to 121 when it is in state 111 P(111 -> 121) (Footnote 2). There are three ways to get to 122, namely, from 111 initially to 121 to 122; from 111 initially to 112 to 122; and from 112 initially to 122. The first way, via 121, is already from a hazard state, hence the system didn't change, this path is already included and one must not count it twice.

Each of the initial states of the universum, (11z) for z = 1,2,3, may occur with probability 1/3. The likelihood of occurrence of (12-) is thus the likelihood of all paths leading to the states 121 and 122 from some initial state (taking care not to count 111 -> 121 twice):

= P(111).P(111 -> 121) + P(112).P(112 -> 122)
= 1/3.1/3 + (P(111).P(111 -> 112) + 1/3).1/3
= 1/9 + (1/9 + 1/3).1/3
= 7/27
Since loss severity is defined to be unity, this means that the hazard level is 7/27.

What is the danger - the likelihood that the hazard state leads to an accident? There's only one accident that can result from the hazard state (12-), namely the event 122 -> 123. The likelihood that 122 leads to the accident is 1/3, as shown in the figure. But the hazard state (12-) comprises not just 122, but includes 121 as well. And the likelihood that the accident occurs from 121 is the likelihood of 121 -> 122 -> 123, which is 1/3.1/3 = 1/9. In any case, the likelihood of an accident resulting by passing through a hazard state is identical with the likelihood of the accident 122 -> 123, since from 121 one must pass through 122 also. This likelihood is again the sum of the probabilities of each path:

P(111 init -> 121 -> 122 -> 123) + P(111 init -> 112 -> 122 -> 123) + P(112 init -> 122 -> 123)
= 1/3.1/3.1/3.1/3 + 1/3.1/3.1/3.1/3 + 1/3.1/3.1/3
= 5/81

It seems intuitively correct to take the risk of the accident 122 -> 123 as being its likelihood, since there is only one loss state 123, and severity is unity. So the risk of the accident 122 -> 123 is 5/81. However, ignoring duration, which for this example plays no role, we are supposed to be able to `combine' hazard level and danger to obtain risk, according to the definitions. Hazard level is 7/27; risk is 5/81. How are we to combine 7/27 with `danger' to get 5/81? Some arithmetical operation is required. Should it be addition? Then `danger' would be (-16/27). Since `danger' is a likelihood, it must be positive or zero. It follows that the operation cannot be addition. Subtraction would yield 16/27. Multiplication would yield `danger' = 5/21. (Division yields 21/5, which being greater than 1 cannot be any likelihood.) It is easy to see that any likelihood, of a path, state or transition, in the graph must have a denominator divisible by 3 and/or 2 only. 21 is 7.3 and therefore does not fulfil this conditions. This rules out the most intuitive operation, that of multiplication, and leaves us with subtraction as the only plausible arithmetic operation to obtain 5/81 from 7/27.

However, it seems completely counterintuitive to suggest that one has to subtract danger from hazard level to obtain risk. I regard this as a reductio ad absurdum of the suggestion that risk of a given accident with resulting severity of unity is obtained by `combining' hazard level with danger. In fact, as we saw, risk is obtained by combining, not the hazard probability, but the individual probabilities of each of the universum states that contain the system hazard state with the individual probabilities for each one of its leading to the accident 122 -> 123.

There is another problem with the definition of risk through hazard. The intuitive concept of risk, given that severity is unity, is the probability that the `specified level of loss', state 123, will occur. Since that state is the result of either of the two accidents 122 -> 123 and 113 -> 123, its probability is the probability that either of the two accidents will occur, namely (since they are independent),

P(123 via 122) + P(123 via 113)
= 5/81 + P(123 via 113)
and
P(123 via 113)
= P(111 init -> 112 -> 113 -> 123) + P(112 init -> 113 -> 123) + P(113 init -> 123)
= 1/3.1/3.1/3.1/2 + 1/3.1/3.1/2 + 1/3.1/2
= 1/54 + 1/18 + 1/6
= 13/54
Hence the probability of 123 is 13/54 + 5/81 = 49/162. Importantly, this includes a component which is obtained by passing through a hazard state, as well as a component from the probability of a behavior which passes through no hazard state before the accident occurs. An accident may happen without passing through a hazard. This shows that any definition of risk through hazard alone is seriously misleading.

Trying To Fix It

 Back to Contents

Consider how we might attempt to fix the definitions. First, let's look at the simplifying assumption that changes cannot be simultaneous. The machine is essentially a serial machine, for example the sequence 111 -> 121 -> 122 -> 123 is three actions, and the universum passes through two intermediate states. Relaxing the assumption could mean that any transition represented by a path could then be taken as one transition; e.g. 111 -> 123. But then the universum does not pass through the intermediate states 121 and 122 (or others). This must therefore be considered a distinct transition, and the system would essentially be a different system. Should we consider it anyway? This relaxation would serve mostly to add possible accidents that occur without passing through a hazard state: 111 -> 123 becomes possible, and since the system state has changed, 111 does not for this reason alone become a hazard state. The arithmetic would become more complicated. I conclude that relaxing this assumption will not help.

Another possible move is to include the loss state 123 as a hazard state. However, no event can happen from this state which would result in a level of loss; all accidents occur before this state, accordingly its contribution to the probability via hazard likelihood calculations would be zero. When calculating hazard likelihood, one would therefore need to combine the likelihood of a hazard state not only with the likelihood of an accident later, but more generally with the likelihood of an accident on a path to or from a hazard state. However, this move would overcount the risk. From the loss state, the likelihood that an accident will occur or has occurred is 1; therefore the extra contribution of considering 123 also as a hazard state will be its likelihood times 1. But this is already the intuitive risk: the separate contributions from the states 121 and 122 are superfluous, and would be counted double if they were counted at all; they should therefore not be explicitly counted as well. It follwos that this suggestion for modifying the hazard calculation simply amounts to the suggestion of calculating the likelihood of 123 by itself; but that was what the hazard calculation was supposed to help us with in the first place. The suggestion is either circular or reduces to triviality.

Another move would be to take the definition of risk as it is given; and conclude that the intuitive concept of risk as (in this case) likelihood of loss given unit severity is not the most appropriate concept of risk. But this is to contradict intuition for the sake of otherwise unmotivated consistency. More particularly, this move falls to a type of argument reminiscent of that of a Dutch book. If I believe my risk is as in the definition, then a series of bets can be constructed such that if I bet according to my judgement of `risk', the bookkeeper is significantly more likely to win. This series is constructed by running the system a large or unbounded number of times, I lose if the system enters the loss state, and I bet according to the inverse probability of my assessment of risk. To avoid probably losing money in the long run, my most rational manoeuvre is to calculate the likelihood of unit loss, what I have called the `intuitive' concept of risk, and bet according to it. If my notion of risk diverges from this, I am very likely to lose. Hence altering the concept of risk also diverts us from the purpose of assessing risk: which is to provide us with a basis for playing this game.

Finally, algebraic calculation using symbolic probabilities (symbols `P(112 -> 122)', `P(123 via 122)', `P(121)' for example, instead of numbers) will soon convince us that there is no algebraic identity using the axioms of probability theory by which we may obtain P(123) from any combination of P(121 or 122) (the hazard probability) and P(123 via (121 or 122)) (the likelihood that 123 will result, given that (121 or 122) has occurred), since the latter reduces to P(123 via 122); and P(122) does not come from 121 alone, but contains a component from 112; and P(123) also contains a component from 113.

I conclude that the situation is not easily rectified.

Alternative Conceptions of Hazard

Back to Contents

It is worth pointing out that the Leveson definition of hazard is counter to a layman's intuitive idea of hazard. While driving my car, I am inclined to call a football bouncing into the road with a child running after it a hazard. I am also inclined to call a pothole in the road a hazard. If I am driving my car in a more or less standard manner, these conditions could lead to - or would inevitably lead to - some sort of accident. It seems to be that the layman's concept calls an environmental state a hazard, if in a given state of the system it would lead to an accident. For example, if I am driving at 0.001 kph, the situations above would not lead to accidents, whereas they would if I am driving at the generally allowable 50kph.

The point of considering and designing for system safety, however, is to avoid environmental conditions leading to accidents. There are two components to this: one is the set of environmental conditions that could contribute; the other is the set of system states that could contribute. The layman's concept calls the former `hazard'; Leveson's concept the latter. Both must be considered. What we call each of them is a matter of denotation only. If we use the layman's concept of hazard for an environmental condition, we would require another term for the system state that contributes. A mere change of terminology, the use of different words, could not avoid the problem that the concepts, environmental condition and system state, do not fit together in quite the way in which Leveson might hope, as I have shown above.

Weakening the Inevitability Requirement

Back to Contents

Other definitions of hazard preserve its feature as a property of system states, but give up the insistence on inevitability. Accordingly, one defines a hazard as a system state that, together with worst-case conditions of the environment, increase the likelihood of an accident to unacceptable levels. There is an element of stipulation in this definition, namely what an unacceptable likelihood of an accident is.

Such stipulations are indeed made; for example, Lloyd and Tye (LT82) explain the various different likelihood categories used in civil aviation certification in the U.K. They note (LT82: Table 4-1) that both U.S. Federal and European Joint Aviation Regulations, in their parts 25, classify events as probable if their likelihood of happening lies between exp(10, -5) and 1, improbable if between exp(10, -9) and exp(10, -5), and extremely improbable if smaller than exp(10, -9); the JARs additionally classify probable events into frequent (between exp(10, -3) and 1) and reasonably probable (between exp(10, -5) and exp(10, -3)), and improbable events into remote (between exp(10, -7) and exp(10, -5)) and extremely remote (between exp(10, -9) and exp(10, -7)). The purpose is (was) to classify an event as extremely improbable if it was unlikely to arise during the life of a fleet of aircraft; extremely remote if it was likely to arise once during fleet life; remote if likely to arise once per aircraft life, and several times per fleet life; reasonably probable if likely to arise several times per aircraft life. Fleet sizes were assumed to be about 200 aircraft, with each aircraft flying 50,000 hours in its life (nowadays, we are seeing fleet sizes are of the order of 1,000 to 2,000, and aircraft flying more than 50,000 hours, altogether about a factor of 10 difference). Effects are also classified into minor, major, hazardous and catastrophic, according to damage, injuries and deaths. The certification basis is (was) to demonstrate that major, hazardous and catastrophic effects could occur at most with remote, extremely remote and extremely improbable frequencies respectively.

The certification basis attempted to assign probabilities to failures, which is prima facie a technique for reliability classification, but in aviation reliability and safety are closely linked. Many system failures, for example, must inevitably entail high risk if not certainty of accident. Multiple engine failures entail that the aircraft must land within a certain radius of its position, whether there is a suitable airport there or no. A fire on board that is not effectively extinguished will spread within a certain time, and be catastrophic unless the aircraft is on the ground at this time. Failure of various specific mechanical parts, or total failure of the flight control system, lead inevitably to an accident. However, reliability and safety may still be distinguished: a recognition light on the underbelly is a safety-critical item; a reading lamp in passenger class is not. The reliability of the latter is not a safety issue.

Could giving up the `inevitability' part of Leveson's definition and replacing it by a specified level of probability avoid the problems? No. No matter what the stipulated likelihood threshold might be, the system state (11-) has the specific likelihood 13/54 that an accident will result, as calculated above. The ultimate purpose of defining the concept of hazard state is to distinguish system states we should pay extra attention to from those which we need not. If 13/54 is larger than our likelihood threshhold, we shall be paying attention to all system states until a state is reached from which an accident is impossible, namely (13-), (21-), (22-) or (23-). So the concept of hazard for S would reduce to the concept of any state from which an accident is at all possible. If 13/54 lies below our threshold, (11-) is not a hazard state, and there remains the accident 113 -> 123 that may occur directly from the non-hazard state. Second, presuming that the precursor system state (12-) remains a hazard state under a change to likelihood, the arithmetic of trying to calculate loss as a function of the likelihood of occurrence of (12-) and any other distinguishable quantity remains impossible. Relaxation of the concept of hazard does not avoid this problem either. The weakening does not help with the problems concerning System S.

Against this, it might be argued that for most actual applications, in which the systems are complex, the weaker notion of hazard is reasonable. But then, I would argue, equally so is Leveson's. Here is the argument. Suppose it were to be useful to consider system states from which there is a high likelihood of an accident occurring. Such a state must be a state in which either (a) there is a high likelihood of an environmental state occurring which leads inevitably to an accident, or (b) there is a high likelihood of a system state occurring that satisfies condition (a). If condition (a) pertains, then the system state is also a hazard state under Leveson's definition. Any effective difference between the two definitions, if there is any, must therefore reside in condition (b).

Consider then condition (b). A hazard state fulfilling (b) but not condition (a) would distinguish itself from the (a)-type hazard by the fact that there is no environmental condition at all under which it would inevitably yield an accident; but there is a likelihood that the system will transition into a state in which there is such an environmental condition. Under the boundary assumption, it makes sense to distinguish (a)-type from (b)-type hazards. For (a)-type hazard states under the boundary assumption, there is little or nothing that one can do to mitigate the hazard. The best thing to do is to avoid (a)-type hazards. However, for (b)-type hazards, under the boundary assumption it would seem appropriate to attempt to hinder the (assumedly unacceptably likely) system transition into an (a)-type hazard state by design. Appropriate engineering attitudes to (a)-type hazards and to (b)-type hazards are thereby clearly distinct, and it makes sense to distinguish them. Whether one calls them `hazard' and, say, `pre-hazard'; or `(a)-type hazard' and `(b)-type hazard', is just a question of naming and is irrelevant to engineering. Accordingly, the weaker notion of hazard has no advantage over Leveson's notion; the distinction must be made anyway.

Giving Up Completely

Back to Contents

A third approach to the definition of hazard is to claim, with John McDermid (McD98p), that it is not possible to give precise definitions of these concepts. Well, that may be so, but in that case their use as fundamental concepts in safety engineering must be suspect. If there can be no precise definition, but they are nevertheless essential concepts, then that means that their appropriate use must remain an art, and reliable guidelines for learning this art must be provided. What are these guidelines and how do they apply to the current example? How do they apply to more complex examples? More particularly, why cannot one write down these guidelines and use them as a definition?

It's important to note that McDermid's claim is more than scepticism. He is not claiming to doubt whether there can be any such definition: he's claiming there cannot be one. The difference can be seen as follows: the sceptic's claim is consistent with being shown adequate, precise definitions; McDermid's claim is inconsistent with it. Does McDermid have a proof that the same engineering goals cannot (I emphasise the modal impossibility claim) be reached through alternative, more precise, concepts and methods? I seriously doubt there can be any such proof; accordingly, the position that there cannot be any precise definition is an article of faith. Furthermore, this faith runs contrary to one of the purposes of engineering, which is to formulate communicable methods by which certain artifactual purposes may reliably be fulfilled; the concepts one uses are at best unequivocal. Without concrete proof, I see no reason to proceed under the assumption that certain essential concepts must remain equivocal (Footnote 3).

Avoidance

Back to Contents

Tom Anderson pointed out to me the series of definitions in (Lap92), which, being mainly concerned with reliability, does not include the concepts of hazard and risk at all. There are some members of WG 10.4, for example Tom's colleague Brian Randell, who take the notion of dependability to include that of safety; this is obviously not the position taken by IFIP WG 10.4 as a whole if (Lap92) is to be the guide.

U.S. Military Concepts

Back to Contents

Ken Garlington pointed out that accidents as normally described can have different losses associated with their outcome (Gar98p), and cited a collision between two military F-16 fighter planes as an example. This would normally be expected to result in loss of life or more than USD1M in damage (a so-called `Class A' mishap in USAF terminology), but such accidents have occurred in which both aircraft returned safely without less than Class A losses. What is going on in this case is that the `accidents' being described are in fact accident types, i.e., classes of accidents with certain features in common. For example, each individual accident will have precisely locatable spatio-temporal features: such-and-such an aircraft part touched another part at a precise time in a precise time zone, in a precise altitude and geographical location (even if these precise coordinates are not so precisely determined). However, classification of accidents for the purposes of safety does not -- cannot, if intended to be predictively useful -- include these features of the accidents. The `accidents' are described by selecting certain state predicates felt to be essential (the collision of two aircraft) and ignoring those felt not to be useful (precise spatio-temporal coordinates). Ergo, accident types are described; and of course accident types may have different outcomes of significance, depending on features which are not included in the predicates describing the type (incidence and relative velocity of, and relative position at, convergence. for example). Thus since losses may differ per accident (type), when calculating overall expected value of loss, ideally one uses a classification category for accidents finer than that of accident type. However, it is not so clear to me that such perfect classifications must exist. However, it suffices mathematically to calculate the expected value of loss from a mishap, and to multiply this by the probability of the mishap, in order to calculate the contribution of this mishap type to the expected value of loss overall. One should, though, take care to ensure that the different mishap categories do not in fact overlap, otherwise one would be counting the contribution of certain incidents multiply.

Ken also pointed out to me that the MIL-STD-882 definition of hazard as a condition that is prerequisite to a mishap (wherein `mishap' is essentially the same as `accident' as we have considered it) does not contain within it the predicate of inevitability. In this form, it could be argued that, since the mishaps 113 -> 123 and 122 -> 123, are distinct, the MIL-STD-882 definition of hazard includes universum state 113 as well as state 122. However, it omits state 121 since this is not prerequisite to a mishap -- the only mishap consequent upon 121 is 122 -> 123, and 121 is not prerequisite to this: the mishap could occur through the sequence 111 -> 112 -> 122 -> 123, in which 121 does not occur.

The MIL-STD-822 definition of `hazard' includes 122 but omits 121. Therefore, it does not a property of a system state, but rather of a universum state. It thus plays a different role from that of Leveson's definition. However, it is not clear that it provides an effective means of determining the expected value of loss. The exact precondition of an accident is a hazard (122 and 112 for System S). Calculating these hazards and multiplying by the expected value of loss per precondition yields the overall expected value of loss. If one is to add in other hazard states multiplied by the expected value of loss from those hazard states, one would be overcounting. This can be seen as follows. Suppose Y is a immediate precondition of accident Acc (such as 122 is the precondition of 122 -> 123, and 112 of 112 -> 123, in S) and let X be some prerequisite of Y -- that is, a state occurring in every behavior that includes Y -- and let us also assume that X occurs in no behavior that results in a mishap other than Acc. Then X is also a hazard. If we are to try to calculate expected value of loss by summing over hazard states multiplied by the expected value of loss from that hazard, then we calculate the expected value of loss through Acc twice: once through considering Y and once through considering X. Hazards according to MIL-STD-822 are not independent events. We must select independent events -- say, enumerating the preconditions Y of accidents Acc and multiplying each by the expected value of loss from Acc. But then the definition of hazard plays no significant role any more -- one might as well enumerate the accidents Acc as their preconditions Y.

Conclusions

Back to Contents

I have shown that, even for a simple case such as system S, in which probabilities are determinate and probabilities of change are independent of history, that even assuming trivial severity and ignoring duration, there are serious problems with the notions of hazard and risk as used about systems. There are three components to this argument:

  1. Risk in the case of unit severity is likelihood of loss;
  2. The risk contributed by an accident occurring from a hazard state cannot be plausibly obtained by any arithmetic combination of hazard level and danger;
  3. There is a component of risk which is contributed by the likelihood of an accident which occurs without the system passing through any hazard state at all; and there are such systems (S is one).
I have also argued that Leveson's definition is an appropriate refinement of alternatives offered in the literature and in standards. However, I do not see how to rescue the definitions given in (Lev95), without giving up the intuitive and compelling interpretation of risk as likelihood of loss, under the assumption that severity is unity; expected value of loss in general. I conclude that the foundations of system safety engineering are logically unsatisfactory and in need of modification.

Acknowledgements

 Back to Contents

I thank members of the hise-safety-critical systems discussion group for their comments and discussion arising from the first version of this paper: Tom Anderson, Peter Bishop, Jens Braband, Bruce Elliott, Ken Garlington, Charles Hoes, Nikola Kanuritch, Nancy Leveson, John McDermid, James Brett Michael, Felix Redmill, Chuck Royalty, Lorne Temes, Ann Wrightson; which discussion led me to add sections Clarifying `Hazard' and Alternative Conceptions of Hazard to elaborate my response to the points they made. I also thank Dirk Henkel and Harold Thimbleby for individual comments.

Footnotes

 Back to Contents

Footnote 1:
I note that Leveson does not explicitly endorse these definitions as her own, simply (we may take it) as her best interpretation of engineering practice. She notes that (Lev95, p171):

[....] terms in system safety are not used consistently. Differences exist among countries and industries. The confusion is compounded by the use of the same terms, but with different definitions, by engineering, computer science, and natural language. [....] An attempt is made in this book to be consistent with engineering terminology [....].
Still, one may doubt that it is in the best interests of engineering to work with incoherent concepts. (Back)

Footnote 2:
I use notation P(xyz) to denote the probability of occurrence of a state xyz in the `run' of the system; since this is logically a temporal event (the system cannot be in this state forever, but only at certain times), this is really shorthand for P(<> xyz), where (<> xyz) is to be read as `eventually xyz', as in temporal logic. P(xyz -> abc) denotes the probability of occurrence of the event (xyz -> abc) given that the system is in state xyz; using the standard notation for conditional probability, it is really a shorthand for P(<>(xyz -> abc) / xyz). P(xyz via abc) is the probability that the system attains state xyz and passes through abc on the way; it is shorthand for P(<> xyz and <> abc). Finally, I use the notation P(11z init -> abc -> .... -> fgh), in which (11z -> abc -> .... -> fgh) is a path, or an initial segment of a path, commencing in the initial state, for the probability of occurrence of this path. (Back)

Footnote 3:
McDermid says he took his view as `axiomatic'. I can't see how that can be the case, considering he must have been aware of Leveson's precise definition of `hazard', as well as many other attempts in the literature and in standards. `Axiomatic' implies `unquestionable', and any attempt at a precise definition must implicitly question the presumption that one cannot be given, especially when that attempt is so public as that of (Lev95). Further, I cannot imagine what any proof, that a precise definition of `hazard' is impossible, would look like. I conclude that McDermid's view doesn't seem to have much support. (Back)

References

Back to Contents

(Gar98p): Ken E. Garlington, private communication, June 16, 1998. (Back)

(KLST71): David H Krantz, R. Duncan Luce, Patrick Suppes, and Amos Tversky, Foundations of Measurement, Volume 1: Additive and Polynomial Representations, New York and London: Academic Press, 1971. (Back)

(Lap92): J. C. Laprie, ed., Dependability: Basic Concepts and Terminology, in ENglish, French, German, Italian and Japanese, IFIP Working Group 10.4, Dependable Computing and Fault Tolerance, Volume 5 in the Series Dependable Computing and Fault Tolerance, Springer-Verlag, 1992.

(Lev95): Nancy G. Leveson, Safeware: System Safety and Computers, Addison-Wesley, 1995. (Back)

(Lev98p): Nancy G. Leveson, private communication, June 12, 1998 (Back)

(LT82): E. Lloyd and W. Tye, Systematic Safety: Safety Assessment of Aircraft Systems, Civil Aviation Authority, London, U.K., 1982. (Back)

(McD98p): John A. McDermid, notes to the safety-critical systems mailing list, June 1998. (Back)

(Sea95): John R. Searle, The Construction of Social Reality, (Back)